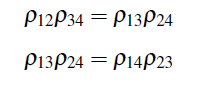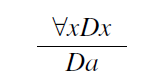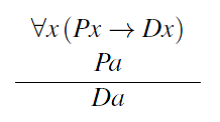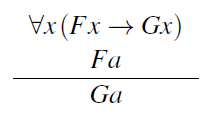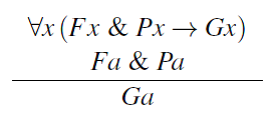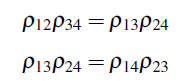Por Clark Glymour
Tradução, notas e comentários de Helkein Filosofia
Um dos modos de argumentar a favor de uma teoria é mostrar uma boa explicação de um corpo de fenômenos e que ela a faz, de fato, melhor do que quaisquer alternativas disponíveis. Esse padrão de argumentação não é limitado pelo tempo ou pelo tema. Podemos encontrar tais argumentações na sociologia, na psicologia, na química e na astronomia desde os tempos de Copérnico até os mais recentes periódicos científicos. A qualidade das explicações é um critério onipresente e em todos os temas científicos constitui um dos principais padrões pelos quais julgamos no que acreditar. A ambição da filosofia da ciência é, ou deveria ser, obter da literatura científica uma teoria plausível e precisa do raciocínio e do argumentar científicos, uma teoria que fará a abstração dos padrões gerais do concreto presente nos debates sobre os genes, espectros e campos. O entendimento filosófico da ciência deve, portanto, nos dar uma explicação de quais são as melhores explicações e por que elas devem ser valorizadas. E o mais importante, também deve nos fornecer critérios claros e plausíveis para que comparemos a qualidade das explicações. Metade do assunto deste ensaio refere-se a um fragmento dessa teoria. Tentarei descrever, sem formalidades ou rodeios, algumas notas que nos forneçam critérios claros e firmes para que julguemos a qualidade das explicações. Isso é metade do meu assunto; o restante trata do modo como esses critérios determinam sobre o que devemos acreditar. Ambas as metades são motivadas pelo livro recente e delicioso de Bas van Fraassen, The Scientific Image.
Onde quer que os teóricos tenham postulado características do mundo que não podiam ser observadas em sua época, surgiram debates sobre a credibilidade científicas da crença no não-observado ou no não-observável. Os debates científicos muitas vezes foram melhor articulados em linhas descartáveis: “Se eu fosse o mestre”, escreveu Dumas na década de 1830 [1], “eu proibiria a palavra ‘átomo’ na química, pois vai além de toda a experiência e nunca, em química, devemos ir além da experiência”. E em nossa própria época, temos o argumento de B. F. Skinner por meio de uma pergunta retórica: quando se tem uma ligação equacional segura entre as variáveis observadas, para quê introduzir variáveis gratuitas não observadas? Também consideramos discussões filosóficas mais ponderadas que levam à mesma opinião, a saber, a de que não há garantias em observações científicas para conclusões que concernam a características não-observadas ou não-observáveis no mundo. Chame aqueles que sustentam tais visões de “anti-realistas” e aqueles que sustentam a visão contrária de “realistas”. Johannes Kepler, J. Dalton e C. Spearman eram realistas; Andreas Oslander, F. Dumas e Skinner eram (e no último caso continua sendo) antirrealistas. [2] O argumento antirrealista foi feito com cuidado e com algo que se aproxima da precisão lógica por vários escritores, mas ainda em nenhum lugar melhor do que o feito por C. G. Hempel, que o argumentou da seguinte maneira: [3] suponhamos que todas as evidências pertinentes ás nossas teorias possam ser formuladas fazendo uso apenas de uma parte da terminologia científica, que chamaremos de “vocabulário observacional”. Por exemplo, Hempel vê a explicação como uma espécie de sistematização dedutiva, e as “conseqüências observacionais” de uma teoria também são sistematizadas – pelos critérios de Hempel, de qualquer maneira – como é a própria teoria (deve-se notar que o próprio Hempel não chegou à conclusão anti-realista, pois esperava que as teorias pudessem proporcionar uma “sistematização indutiva” inatingível sem elas.) Além disso, Duhem [4] e Quine argumentaram que, uma vez que consideremos hipóteses que transcendam toda experiência possível, entramos no campo da convenção e da arbitrariedade, pois as evidências e os cânones do método científico só podem determinar o que devemos acreditar sobre o observável, visto que o inobservável é indeterminado: uma pletora de conjecturas alternativas explicará a evidência igualmente bem. Reivindicações do mesmo tipo foram feitas contra a teoria de Dalton por seus oponentes anti-atomistas – as propriedades dos átomos, disseram eles, são indeterminadas e arbitrárias.
Duhem, Quine e outros têm razão, se permitirmos à ciência apenas uma coleção suficientemente empobrecida de princípios de avaliação e inferência. Mas até os critérios fragmentários da explicação científica são suficientes para que eu derrote os argumentos anti-realistas. Pois, embora os critérios não utilizem a noção de observabilidade, eles produzem o resultado de que, às vezes, a melhor explicação vai muito além do que é observado ou observável. Ou, para colocar algo mais à moda de Hempel, os critérios produzem o resultado de que às vezes uma teoria dotada de “termos de não-observação” possui virtudes explicativas que são impossíveis de se obter sem tais termos, além de que tais critérios de comparação de explicações não nos envolvem em indeterminações aos nos levarem para além do observável. Inversamente, em certos contextos, basta determinar uma melhor teoria unificada que explique devidamente os fenômenos. Além disso, nada há acerca desses critérios determinantes da qualidade explicativa que exija ou pressuponha que sejam aplicadas apenas as teorias que contenham afirmações sobre o que é inobservável. Os mesmos critérios são usados para determinar as melhores teorias concorrentes sobre as características observáveis do mundo. Os mesmos critérios às vezes determinam – pelo menos até onde entendo a noção de “observabilidade” – que as teorias que estão confinadas às características observáveis do mundo são melhores explicadores do que os concorrentes que postulam características não-observáveis. Tudo isso me parece exatamente como deveria ser. O resultado é simplesmente que as mesmas características de inferência que levam a conclusões gerais sobre o observável também levam em outros contextos a determinar conclusões sobre o não-observável. Consequentemente, acredito que existam apenas duas maneiras de manter a posição anti-realista: empobrecendo (talvez eu deva dizer emasculando) os métodos da ciência e proibindo critérios totalmente explicativos – como aqueles que descreverei – ou arbitrariamente (e vagamente) restringindo o escopo de aplicação de tais princípios à esfera do observável.
II
Em discussões sobre explicações científicas e os fundamentos que essas explicações possam nos dar acerca da crença em aspectos não-observáveis no mundo, é importante manter em mente os casos reais. Eventualmente, tentarei mostrar que todos os casos a seguir possuem algo importante em comum:
- A explicação copernicana sobre a regularidade dos astros superiores, e em particular a regularidade observada por Ptolomeu, que se em um número inteiro de anos solares um astro superior passa por um número inteiro de oposições e também por um número inteiro de revoluções de longitude, então o número de anos solares é igual ao número de oposições mais o número de revoluções de longitude. A teoria copernicana explica a regularidade observando que o número de anos solares é igual ao número de revoluções que a Terra fez em torno do sol e que o número de oposições é igual ao número de vezes que a Terra, movimentando-se mais rápido, ultrapassou o astro superior que se move mais lentamente em uma órbita fora da órbita da Terra, e também que o número de revoluções de longitude é igual ao número de revoluções que o astro superior fez sobre o sol.
- A explicação daltoniana da lei das proporções definidas. A lei afirma que, em dois casos em que quantidades dos mesmos reagentes químicos puros se combinem para produzir certa quantidade dos mesmos produtos, as proporções dos pesos combinados dos reagentes são as mesmas. A explicação de Dalton é que qualquer amostra de uma substância química pura consiste em moléculas, cada uma tendo o mesmo peso que qualquer outra, e que cada molécula de um determinado tipo é composta pelo mesmo número de átomos de vários tipos. Todos os átomos do mesmo tipo têm o mesmo peso, e uma reação química é apenas um processo no qual os átomos constituintes das moléculas nos reagentes são recombinados para formar as moléculas dos produtos. Assim, as proporções dos números de moléculas dos vários reagentes que se combinam são invariantes e característicos da reação. Duas amostras diferentes de reagentes com pesos diferentes diferem no número de moléculas que eles contêm, mas como o peso de qualquer amostra pura é apenas a soma dos pesos de suas moléculas constituintes, a proporção dos pesos dos reagentes será igual à razão do número de moléculas que elas contêm.
- A explicação relativística geral do movimento anômalo do periélio de Mercúrio e da deflexão da luz das estrelas passando perto do escurecimento de bordo do sol. As explicações são mais ou menos as seguintes: para campos gravitacionais fracos, como os dos planetas a distâncias astronômicas, a teoria da relatividade se aproxima da teoria gravitacional newtoniana. Portanto, no caso de Mercúrio, bem como no caso da luz das estrelas, a única contribuição significativa para o campo gravitacional é a do sol, que é conhecido por ser esférico. Portanto, o campo gravitacional é, para uma boa aproximação, o campo gravitacional de um único ponto de massa. A partir das equações de campo da teoria, o campo gravitacional, no espaço vazio, de um único ponto de massa é determinado exclusivamente e descreve a geometria do espaço-tempo circundante. As equações de movimento da teoria implicam que os raios de luz se movem sobre a geodésica nula dessa geometria e as partículas maciças se movem sobre a geodésica do tempo. A luz de uma estrela pode ser descrita como um raio, e o planeta Mercúrio reage à gravidade (a uma boa aproximação) como uma massa pontual. Dadas as condições iniciais, seguem-se os fenômenos.
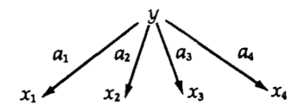
- A explicação de Spearman das correlações entre os testes de inteligência. Embora a história seja complicada, provavelmente é justo dizer que Spearman inventou a análise fatorial quando, em 1904, ele publicou dois artigos, um sobre a medição de correlações e outro sobre a medição da inteligência. [5] Spearman obteve várias avaliações da população infantil em idade escolar, incluindo avaliações de “inteligência” e de discriminação sensorial. Analisando seus dados de 1904 e mais tarde, ele argumentou em suas análises de habilidades humanas que, para qualquer uma dessas quatro medidas, digamos X1, X2, X3, X4, as correlações entre as medidas desaparecem em “diferenças tetrádicas”. Ou seja, empiricamente, verifica-se que, para qualquer quadruplo de medidas para suas amostras:
Onde Pij for a correlação entre Xi e Xj. Spearman afirmou que a melhor explicação para essas equações é que existe um fator comum que determina os resultados das pontuações em todas as medidas, e ele chamou esse fator de “inteligência geral”.
Esses casos mencionados acima não são essenciais para qualquer teoria da explicação, mas como casos eles têm virtudes importantes. Eles representam uma série de assuntos, são explicações que têm um papel histórico genuíno e não foram usados para satisfazer a curiosidade ociosa – como nas perguntas sobre bolhas de sabão –, mas foram peças cruciais dos argumentos dados para as respectivas teorias. Eles também não têm conexão uniforme com distinções entre o que é observável e o que não é. A teoria copernicana postulava características – os movimentos dos planetas no espaço tridimensional – que não podiam ser observados no século XVI. O mesmo fizeram as teorias concorrentes. No entanto, alguns desses recursos podem ser considerados, hoje, observáveis. A teoria atômica de Dalton certamente concernia a características do mundo que serviram quase como casos paradigmáticos do não-observável. Não tenho idéia se o campo métrico do espaço-tempo deve contar como observável ou como não-observável. A “inteligência geral” de Spearman é certamente uma característica não-observável das pessoas – com mais cuidado, uma vez que se pode duvidar que exista tal coisa, se houvesse um fator como a inteligência geral de Spearman, seria inobservável. Os fenômenos explicados nesses casos podem ser vistos às vezes como regularidades, às vezes como eventos particulares ou sequências de eventos e às vezes como ambos. A regularidade dos planetas superiores é de fato uma regularidade, mas a teoria copernicana também explica todas as instâncias do fenômeno. O mesmo vale para proporções definidas e o movimento de Mercúrio.
A explicação da deflexão da luz foi, de fato, a explicação de alguns eventos, mas há uma regularidade correspondente que a teoria explica. As equações de Spearman não descrevem eventos particulares nem expressam generalizações; suponho que eles sejam melhor compreendidos como expressando características particulares da população testada. Finalmente, para cada uma dessas explicações, havia uma teoria alternativa gerando explicações concorrentes. O ponto alto dos argumentos científicos era que as explicações citadas eram melhores do que quaisquer outras disponíveis. As explicações copernicanas foram comparadas às explicações ptolemaicas, as explicações relativísticas gerais com as clássicas e os relatos de um fator das correlações foram comparados com os relatos multifatoriais.
III
Creio que um dos principais objetivos de uma investigação filosófica sobre os aspectos da explicação científica seja o fornecimento de um ou mais cânones que sirvam para avaliar teorias científicas. Até onde sei, a literatura filosófica sobre a explicação científica não fornece critérios claros que sirvam para explicar por que os casos que citei podem ser vistos como explicações satisfatórias ou, particularmente, por que deveriam ser vistos como melhores do que explicações alternativas. Entretanto, o que tenho a fornecer por meio de critérios está intimamente ligado a algumas articulações filosóficas da noção de explicação científica.
As teorias filosóficas sobre a explicação científica podem ser divididas em três tipos: teorias puramente lógicas, que analisam a explicação apenas em termos de relações lógicas e condições de verdade; teorias com estrutura objetiva extra, que impõem condições objetivas à explicação além daquelas da verdade e da estrutura lógica; e teorias com estrutura subjetiva extra, que impõem explicações às condições psicológicas de crença, interesse e assim por diante. [6]
O aparente objetivo de Hempel e Oppenheim [7] foi fornecer um estudo da estrutura lógica da explicação na linha da tradição lógica de Frege, Russell, Whitehead e Hilbert, que proveu resultados sobre a estrutura lógica da “prova de”. As condições dadas por Hempel e Oppenheim não intentaram ser uma análise de quando era apropriado dizer quando alguém explicou alguma coisa; entretanto, elas intentaram especificar a estrutura lógica explícita presente em explicações não-estatísticas que as ciências naturais normalmente mantêm implícitas caso tenham alguma. Se Hempel e Oppenheim fossem bem-sucedidos em seus objetivos, seus critérios teriam formulado um padrão crítico para julgar teorias e hipóteses. Baseando-se apenas na estrutura lógica, determinariam totalmente quais sentenças singulares uma dada teoria poderia potencialmente explicar e quais não poderia. Combinadas a um estudo adicional de como utilizar as informações sobre o que as teorias poderiam ou não explicar em seu método avaliativo, um estudo lógico como o de Hempel e Oppenheim prometeu promover um entendimento de como a explicação é usada para que decidamos o que aceitar e em que acreditar.
A explicação de Hempel e Oppenheim da estrutura lógica das explicações dedutivas revelou-se totalmente inadequada para sua tarefa. Com efeito, dada uma sentença E arbitrariamente verdadeira (mas não logicamente verdadeira) e uma sentença S universalmente quantificada arbitrária que não é uma verdade lógica, existe uma consequência lógica de S e uma sentença singular C verdadeira, de modo que a consequência lógica de S e C juntas constituem as premissas de uma explicação potencial de E. [8] Com efeito, qualquer coisa explica qualquer coisa. O que era importante no trabalho de Hempel e Oppenheim não era a execução, mas a visão. Se alguém compartilha a visão, a resposta natural ao fracasso de sua análise é tentar outra do mesmo tipo, em termos inteiramente lógicos ou, talvez, com estrutura extra.
Várias substituições puramente lógicas para a análise de Hempel e Oppenheim foram publicadas. Embora nem todas sejam triviais, elas são, sem exceção, muito fracas para fornecer critérios úteis para a avaliação da teoria. Talvez a melhor tentativa seja a de David Kaplan, [9] que usa condições de verdade e também estrutura lógica para restringir a explicação.
Estudos como o de Kaplan são deficientes em tolerar como explicações uma série de casos que rejeitaríamos como não explicativos. Para qualquer explicação na forma:
Se P é qualquer propriedade que o indivíduo a também possui, então:
É uma explicação que atende aos critérios de Kaplan e, da mesma forma, várias generalizações dos critérios de Kaplan. Novamente, para qualquer explicação na forma:
Se P é qualquer propriedade que o indivíduo a também possui, então:
É também uma explicação que atende aos critérios do estudo de Kaplan. Assim, para usar um exemplo de Henry Kyburg, podemos explicar o fato de que uma amostra de sal de mesa se dissolve na água citando a (verdadeira) alegação de que a amostra de sal de mesa foi enfeitiçada e a (verdadeira) generalização de que todos os sais de mesa enfeitiçados se dissolvem na água.
Uma resposta sensível a essas dificuldades é que elas não mostram nada além da incompletude da análise da explicação. Assim, para uma descrição da natureza de Kaplan, restrita à forma lógica das explicações, deve-se adicionar critérios para comparar explicações com a forma lógica apropriada. Por exemplo: quando existe uma explicação da forma (1), quaisquer explicações na forma (2) são preteridas. Como alternativa, podem-se reconstruir as condições lógicas da explicação para que (2) e (4) não contem como explicações. Wesley Salmon propõe considerar a explicação dedutiva como um caso extremo da explicação estatística; [10] explicar um único evento consiste em atribuí-lo a um membro de uma partição estatisticamente homogênea da maior classe de eventos que pode ser particionada. Muito habilmente, segue-se que quando (1) é bem-sucedido, (2) não atende às condições de explicação (a menos que P e D sejam coextensivos), e algo análogo ocorre com (3) e (4).
Nenhum desses trabalhos sobre explicações fornece critérios que possam ajudar a explicar os casos mencionados anteriormente ou outros do mesmo tipo. As teorias astronômicas ptolomaicas e copernicanas forneceram deduções de sentenças sobre as posições dos planetas a partir de sentenças gerais de jure; se isso for o necessário para uma possível explicação, as duas teorias a forneceram. A teoria atômica explicava cada instância da lei de proporções definidas, mas, no que se refere a esses critérios lógicos, foram obtidas explicações igualmente boas do ponto de vista, popular no século XIX, de que se deve abjurar átomos e simplesmente criar tabelas de pesos combinantes. Comentários semelhantes são válidos para outros casos. O relato explicativo de Salmon, é justo dizer, é tal que simplesmente não sabemos como aplicá-lo nesses tipos de contextos.
Uma maneira simples de ver as limitações dos critérios dedutivos descritos até agora é considerar o que seria explicar uma regularidade em vez de um único evento. Naturalmente, supõe-se que explicar uma regularidade é explicar todas as suas instâncias, mas, se nada além for necessário, toda regularidade é autoexplicativa. Se exigirmos ainda que o que explica uma regularidade não seja logicamente implícito pela própria regularidade, a situação ainda não melhora, como observaram Hempel e Oppenheim, pois continuará sendo o caso de que, por esses critérios, quaisquer regularidades possam ser explicadas ao conjugá-las com quaisquer outras logicamente pendentes.
Não conheço escritor algum que tenha tentado considerar apenas a explicação das regularidades em termos lógicos. Inevitavelmente, outras considerações além da verdade e da forma lógica entram nos critérios, e isso é bastante apropriado e inofensivo, desde que a estrutura adicional não derrote o próprio objetivo de uma descrição da explicação – ou seja, para nos ajudar a entender como a explicação pode ser e é usada para avaliar nossas hipóteses. Três discussões recentes sobre a explicação que apelam para a estrutura extra são especialmente valiosas, não tanto por quaisquer avanços técnicos que façam, mas por apontar para características da explicação facilmente ignoradas e por pelo menos sugerir que essas características podem ser formalmente tratáveis. Uma é a proposta de Michael Friedman de que o que boas explicações teóricas fazem é de alguma forma reduzir o número de hipóteses que devem ser aceitas independentemente uma da outra [11]. A outra é a cuidadosa análise de Robert Causey da estrutura das reduções inter-teóricas, [12] com ênfase na identidade dos objetos e propriedades descritas e postuladas pelas hipóteses a serem explicadas com complexos de objetos e propriedades postuladas pela teoria que fornece a explicação. A terceira é a tentativa de Baruch Brody de trazer Aristóteles de volta à explicação científica [13] e de levar a sério a ideia de que boas explicações científicas mostram que o evento ou a regularidade a ser explicada são necessários, não apenas uma conseqüência necessária de pressupostos teóricos. Nenhum desses três relatos é suficiente para tratar os tipos de casos que descrevi anteriormente, e apenas o de Friedman realmente constitui uma tentativa de fazê-lo. No entanto, a tentativa de Friedman desmoronou; A análise de Causey tem dificuldades técnicas e não fornece critérios comparativos aplicáveis; e o relato explicativo de Brody pode ser aplicado para comparar afirmações concorrentes para explicar um fenômeno apenas nas situações em que sabemos, independentemente, algo sobre quais propriedades são essenciais e quais são acidentais. Mesmo assim, em cada um desses três casos, os motivos parecem sólidos à sua maneira, e o esquema que apresento abaixo pode ser visto como uma tentativa de unificar os aspectos de cada um deles.
IV
Uma das coisas que muitas explicações parecem fazer, e que apela a certas intuições sobre explicações, é demonstrar que um fenômeno é realmente apenas uma variante ou uma manifestação diferente de outro fenômeno. Em algumas ciências, as explicações fornecidas nos livros didáticos são geralmente desse tipo. Na termodinâmica clássica, por exemplo, o exercício padrão repetido ao longo de livros didáticos de físico-química consiste em usar princípios termodinâmicos para derivar regularidades empíricas umas das outras. A primeira e a segunda lei são usadas para derivar a lei de Joule da lei ideal dos gases ou para derivar da lei dos gases o fato de que o calor específico em pressão constante menos o calor específico a volume constante é proporcional à constante de gás. Intuitivamente, uma explicação produz uma forma de compreensão se nos mostrar que o fenômeno que queremos explicar é uma manifestação de um fenômeno diferente que já conhecemos. O entendimento consiste em compreender a unidade dos padrões ou a substância por trás de fenômenos aparentemente díspares. Em contextos físicos, a mecânica de tais explicações é familiar a qualquer pessoa que tenha sofrido com conjuntos de problemas. No caso termodinâmico, começa-se, digamos, com Cp – Cv = R e explica essa relação relacionando uma subfórmula (por exemplo, Cp – Cv) a quantidades termodinâmicas, aplicando as leis termodinâmicas a essas quantidades e obtendo o resultado que Cp – Cv = PV / nT. [14]
Como primeira tentativa de um estudo formal desse recurso de explicação, considere as teorias representadas no cálculo de predicados. Por conveniência, suponhamos que todas as frases consideradas estejam na forma de prenex. Consideremos uma subfórmula de uma frase S qualquer subfórmula bem-formada que ocorra na matriz da forma prenex, que não seja logicamente equivalente à frase inteira. Uma subfórmula de uma frase pode ter várias ocorrências em uma frase. Por um termo em S, queremos dizer qualquer termo que ocorra na matriz de S. Digamos que, onde T, H e K são sentenças, T explica H como resultado de K se for para subfórmulas (não válidas) H1… HN de H, nenhuma das quais ocorre em H como subfórmulas de nenhum dos outros, e os termos t1,.., tk de H, não ocorrem em H1… HN , existem fórmulas K1… KN termos S1…, Sk e subteorias T1,…, Tn + k, de T de modo que
A terceira condição acima é natural e necessária para a eliminação de explicações falsas. Por exemplo, não se poderia usar nenhuma teoria, incluindo a lei dos gases ideais, para explicar essa mesma lei como uma forma da relação T = T (onde T é a temperatura) iniciando com PV = nRT e observando que a partir da teoria segue que PV/nR = T e que ao substituir T por PV/nR, na lei dos gases ideais, obtém-se T = T. Tal explicação é excluída pela condição (iii). A condição pela qual um termo substituído não ocorre como parte de uma subfórmula substituída talvez seja indevidamente restritiva, mas se destina a evitar complicações.
Na prática, geralmente não consideramos fórmulas de primeira ordem, mas equações representando teorias que devem fornecer as explicações. Nesse contexto, T explica H como resultado de K, onde H (X1, …, XN) = 0 e K (Y1, …, Ym) = 0 são equações e T um sistema de equações, e se há consequências Ti de T, não envolvendo H, e cada Ti implica uma equação entre uma combinação dos Xs que ocorrem em H e uma combinação de Ys, e quando as combinações de Ys são substituídas em H pela combinação correspondente de Xs, obtém-se uma equação que é satisfeita sempre que K está presente.
Como apresentei essas condições, elas não satisfazem a condição de equivalência lógica; isto é, T pode explicar H como resultado de K, enquanto que para as fórmulas logicamente equivalentes T’, H’ e K’, T‘ falha em explicar H’ como resultado de K’. Obviamente, o que quero dizer é que T explica H como resultado de K se cada uma dessas sentenças possui equivalentes que atendam às condições formais. De fato, a equivalência é geralmente muito mais ampla que a equivalência lógica, pois contamos uma equação H, explicada como resultado de K, se pudermos encontrar equivalentes matemáticos de H e K atendendo às devidas condições. Sem dúvida, a proposta formal também apresenta outros defeitos; é, na melhor das hipóteses, uma primeira tentativa. Espero que os veteranos da tradição dos livros didáticos de física e química sejam pelo menos lembrados de que grande parte do trabalho nas explicações apresentadas e nos problemas atribuídos foi encontrar as representações corretas das equações e as subteorias corretas, a fim de derivar uma coisa da outra.
Uma teoria pode envolver cada membro de uma classe de regularidades sem explicar nenhum deles como resultado de qualquer outro. Se, por exemplo, as regularidades em questão são logicamente (matematicamente) independentes, a teoria que consiste em sua conjunção terá essa propriedade. Assim, para emprestar um exemplo de Friedman, a teoria que consiste na conjunção dasdas leis de Kepler, da lei de Boyle, da lei de Galileu sobre corpos em queda e da lei do pêndulo não explica nenhuma dessas regularidades como resultado de qualquer outra. Novamente, a conjunção da aditividade de massas e a lei de proporções definidas não explica nenhuma dessas regularidades pela outra. Por outro lado, a teoria atômica explica a lei de proporções definidas como resultado da aditividade das massas, e essa unificação é uma das grandes virtudes da teoria. Em alguns contextos em que as teorias estão sendo avaliadas e comparadas, há uma coleção razoavelmente bem estabelecida de regularidades empíricas logicamente independentes pertinentes à avaliação. Teorias conflitantes, como a teoria atômica e a teoria dos equivalentes, podem muito bem envolver uma classe comum de regularidades, mas as classes de regularidades pertinentes às respectivas teorias não precisam ser coextensivas: a aditividade das massas não tem nada a ver com a teoria de equivalentes, mas muito a ver com a teoria dos átomos. Em geral, preferimos teorias que expliquem regularidades implícitas como o resultado de outras regularidades estabelecidas para teorias que não o fazem. Mais exatamente, proponho o seguinte princípio bastante modesto de comparação:
- Ceteris Paribus se T e Q são teorias e para cada par estabelecido de regularidades, H, K, de modo que Q explica H como resultado de K, T também explica H como resultado de K, mas existem regularidades estabelecidas, L, J, de modo que T explica J como resultado de L, mas Q não explica J como resultado de qualquer outra regularidade estabelecida, T é preferível a Q.
A afirmação é complicada, mas a idéia é quase trivial e me parece fazer parte do que é correto sobre a sugestão de Friedman de que boas teorias reduzem o número de hipóteses independentemente aceitáveis. Pode ser interessante explorar outros princípios de comparação que se estenderiam a circunstâncias nas quais teorias concorrentes explicam um conjunto comum de regularidades como resultado de outras regularidades, mas discordam sobre quais regularidades são o resultado de outras regularidades. Deixo o assunto de lado, exceto por um caso especial a ser discutido mais adiante.
Há dois pontos a serem enfatizados. Primeiro, de acordo com o princípio 1, certas teorias implicando regularidades empíricas podem ser totalmente preferíveis à conjunção dessas regularidades sozinhas, e podem ser também preferíveis à conjunção de regularidades implícitas com quaisquer regularidades que possam ser alegadas como resultado destas. A teoria atômica ilustra o ponto. Segundo, de acordo com o princípio I, a teoria copernicana é preferível à sua principal rival, a astronomia ptolomaica, e a explicação de Spearman das equações de correlação entre quatro variáveis medidas em termos de um único fator comum é preferível a muitas explicações alternativas que salvam igualmente os fenômenos. Para ver isso, ajudará o retorno à ideia de Brody.
Pelo menos parte dos ideais de Brody de que podemos explicar um estado de coisas mostrando que ele é necessário, e que tal demonstração deve ser feita mostrando que o estado de coisas é uma consequência lógica das propriedades essenciais das entidades envolvidas, e das leis que governam essas propriedades essenciais. Sugiro um tipo diferente de demonstração de necessidade: podemos mostrar que uma regularidade tem um tipo de necessidade, explicando-a como resultado de uma verdade necessária. Em particular, no esquema de “T explica H como resultado de K”, nada proíbe que K seja uma verdade lógica ou matemática e, portanto, necessária. As verdades lógicas e matemáticas, em geral, podem ser consideradas regularidades e certamente podem ser estabelecidas e usadas na avaliação de teorias. No caso da astronomia posicional copernicana, e no caso das tétrades de Spearman, as regularidades ou equações de tipo empírico são explicadas como resultado de verdades matemáticas.
É uma verdade matemática que se dois objetos se moverem em órbitas fechadas sobre um centro comum, uma órbita dentro da outra, e o objeto interno se move mais rápido que o objeto externo, então o número de rotações do objeto interno é igual ao número de rotações do objeto externo mais o número de vezes que o objeto interno ultrapassou o objeto externo, sempre que todos esses números forem inteiros. Segundo a teoria copernicana, a Terra se move em uma órbita interior para a órbita de qualquer planeta superior e se move mais rapidamente em sua órbita do que um planeta superior. O número de anos solares é igual ao número de revoluções da Terra em sua órbita; o número de oposições ou ciclos de anomalia é igual ao número de vezes que o planeta superior é ultrapassado pela Terra e (durante qualquer longo período) o número de revoluções de longitude de um planeta superior é igual ao número de revoluções em sua órbita. Assim, a regularidade planetária observada por Ptolomeu é explicada pela teoria copernicana como resultado de uma verdade matemática. Não é explicado na teoria ptolomaica como resultado de qualquer outra regularidade estabelecida independentemente.
Spearman assume (tacitamente) que as relações entre variáveis medidas e fatores não medidos são lineares. Assumindo que o erro de medição seja em média igual a zero e que os erros nas variáveis medidas não sejam correlacionados entre si, segue-se que, para variáveis padronizadas, a correlação entre duas variáveis é igual ao produto dos coeficientes lineares que relacionam cada variável do par ao fator comum. Assim, com o esquema causal de Spearman:
Nós temos:
Substituindo o lado direito dessa equação segundo as suposições da equação empírica de Spearman…
Obtemos exemplos de verdades triviais da álgebra real. Assim, as equações de tétrade de Spearman são explicadas como resultados de verdades matemáticas. Normalmente, podem ser encontrados outros arranjos de fatores não medidos que são consistentes com as equações de tétrade, mas isso não explica as equações de tétrade como resultado de verdades matemáticas.
Alguém pode se perguntar se, nos casos copernicanos e psicométricos, uma regularidade empírica foi inteiramente explicada como resultado de verdades necessárias, pois as relações copernicanas entre números de órbitas e revoluções na longitude e nos anos solares, e assim por diante, pelo menos, não são verdades necessárias. Mais uma vez, equações psicométricas que relacionam coeficientes de correlação a “líderes de fatores” dificilmente parecem verdades necessárias.
Suponho que, sendo outras coisas iguais, preferimos explicações de regularidades em termos de verdades necessárias a explicações dessas mesmas regularidades em termos de outras generalizações empíricas. Suponho ainda que consideremos particularmente virtuosas as explicações das regularidades como resultado das verdades necessárias e o fazem por meio de conexões que são elas próprias necessárias. Quando essas explicações são bem-sucedidas, elas são completas e nada permanece sendo necessário. Não pretendo sugerir que uma ou todas essas considerações esgotem os critérios pelos quais julgamos explicações. É por isso que existem cláusulas ceteris paribus. Era verdade, é claro, que uma das principais razões para a inferioridade das explicações newtonianas do avanço do periélio e da deflexão da luz era que todas essas explicações exigiam circunstâncias hipotéticas – massas ocultas e concentrações de éter – para as quais não havia evidência alguma.
V
O princípio explicativo fornece uma razão pela qual, em cada um dos casos descritos na seção II, a explicação é particularmente virtuosa e por que é melhor do que as explicações concorrentes. Em alguns desses casos, há até uma pequena evidência histórica de que essas virtudes foram reconhecidas em algo como a forma que são dadas aqui: Kepler elogiou a teoria copernicana em contraste com a astronomia ptolomaica, porque a primeira faz das regularidades dos planetas uma “necessidade matemática”. Em cada um dos casos considerados, o poder explicativo é obtido através da introdução de conexões e estruturas teóricas não explícitas nas regularidades a serem explicadas, e em cada um desses casos as conexões entre regularidades empíricas não poderiam ser feitas sem estrutura teórica adicional. A regularidade dos planetas superiores simplesmente não pode ser explicada como resultado de uma verdade matemática, a menos que as quantidades que ocorrem na declaração dessa regularidade estejam de alguma forma relacionadas a outras quantidades distintas de anos solares, oposições e revoluções de longitude.
O mesmo se aplica às equações da tétrade de Spearman e ao movimento de Mercúrio, e assim por diante. A lei de proporções definidas não pode ser explicada como resultado da aditividade da massa, a menos que se introduzam objetos que não sejam as amostras macroscópicas de elementos que foram utilizados no laboratório do século XIX. Em alguns desses casos, a estrutura adicional que deve ser introduzida para obter as conexões explicativas é a estrutura que se tornou observável; em outros casos, essa estrutura não se mostrou inobservável, ou pelo menos indiscutivelmente inobservável. Mas a observabilidade ou a falta dela não tem nada a ver com a virtude explicativa em questão. Parece não haver motivos, exceto os arbitrários, para o uso de um princípio de preferência para dar credibilidade às afirmações teóricas quando as afirmações se referem a características observáveis do mundo, além de reter credibilidade quando as afirmações teóricas obtidas pelo mesmo princípio acaba sendo sobre características não observáveis do mundo. O argumento para átomos é tão bom quanto o argumento para órbitas. Conheço três objeções a esse argumento: primeiro, essa explicação é subjetiva e dependente do contexto e, portanto, não pode ser um fundamento objetivo e interpessoal para a crença; segundo, que o princípio de preferência apresentado na seção IV pode ser aceitável como um princípio que rege em quais teorias devemos preferir aceitar, exibir ou trabalhar, mas não pode ser aceitável como um princípio que governa em quais teorias devemos preferir acreditar; e terceiro, que a introdução da estrutura teórica além dos limites da observação gera indeterminação sem limites.
Muitos escritores sustentam que a explicação é basicamente uma noção pragmática. A relação explicativa fundamental é considerada algo da forma ‘X explica Y para pessoa P’. Obviamente, o que explicará Y para a pessoa P dependerá do que P já sabe sobre Y, não sabe sobre Y, quer saber sobre Y e assim por diante. Essa visão da explicação é cercada por exemplos que trocam as ambiguidades de “perguntas sobre o porquê” e a dependência de contexto de respostas relevantes a perguntas do tipo “o que causa Y?”. Sem dúvida, o entendimento é uma noção pragmática e, sem dúvida, legitimamente chame de “explicações” essas respostas para “perguntas sobre o porquê” (e perguntas de outras formas) que produzem entendimento na audiência. Nada disso é pertinente para a existência ou não de relações objetivas e não pragmáticas entre teorias e afirmações de fenômenos empíricos, relações que, quando apreendidas, produzem entendimento e fundamentam a crença. A afirmação de que a explicação é inteiramente dependente de interesses tem exatamente tanto mérito quanto a afirmação de que “prova” é inteiramente dependente de interesses: com base no que o público matemático de alguém sabe ou acredita, diz-se algumas coisas ao fornecer provas, mas não outras; existem argumentos que atendem às condições formais de prova, mas que não chamamos de provas porque são desinteressantes (por exemplo, porque não temos motivos para acreditar nas premissas, como na “prova” da conjectura de Poincaré das premissas que (1) Glymour pesa mais de 190 libras e (2) se Glymour pesa mais de 190 libras, então a conjectura de Poincaré é verdadeira). Um relato de “prova” inteiramente ligado ao discurso e evitando a caracterização da forma lógica ideal seria ofuscante; o mesmo seria uma explicação da explicação.
Bas van Fraassen argumentou que as preferências do tipo para as quais apelei em princípio não podem ser credenciais ou preferências quanto ao que acreditar. A razão é a seguinte: De acordo com princípios como i, a teoria copernicana, por exemplo, deve ser preferida à conjunção das leis empíricas que ela explica. Mas a conjunção das leis empíricas explicadas pela teoria copernicana é uma consequência lógica da teoria copernicana. Não podemos razoavelmente dar mais crédito a uma reivindicação do que a suas consequências lógicas. Portanto, as preferências em princípio não podem ser credenciais ou preferências por crença.
Van Fraassen está certo, no que se refere a isso, mas as preferências podem, no entanto, estar ligadas à crença. Pode ser irracional acreditar em uma coleção de leis empíricas, acreditar que uma teoria específica implica essas regularidades, é testada por elas e as explica melhor do que qualquer outra teoria possível, e ainda não acreditar na teoria. A irracionalidade é semelhante à de acreditar em certas premissas, acreditando que alguma outra sentença é uma consequência lógica dessas premissas, e recusando, no entanto, em acreditar na sentença adicional. Há tanto um fechamento indutivo quanto um fechamento dedutivo. A preferência declarada no princípio 1 é uma preferência para um certo candidato ao fechamento indutivo das regularidades explicadas. Se a teoria T é preferível à teoria Q, de acordo com o princípio 1, isso não significa que se deva acreditar em T em vez de Q, ou que haja razões para acreditar em T em vez de Q, pois Q pode ser um argumento lógico consequência de T. Em vez disso, a preferência deve ser entendida como significando que o fechamento indutivo das leis explicadas é (o fechamento dedutivo) da teoria T, em vez de (o fechamento dedutivo da) teoria Q. Mais simplesmente, mas menos exatamente, a preferência é acreditar em T em vez de acreditar meramente em Q, quando T e Q são consistentes, ou por acreditar em T, em vez de Q, quando T e Q não são consistentes.
Há alguns anos atrás, Quine argumentou que, uma vez que introduzimos uma linguagem que não descreve características observáveis do mundo, a subdeterminação é galopante. “Galopante” significa infinito aqui, pois se apenas um número finito de teorias é consistente com todas as evidências possíveis de algum tipo e satisfazem nossos cânones indutivos, então há uma conclusão preferida, a saber, sua disjunção. Tais visões amplas não são convincentes, pois carecem de uma explicação convincente da equivalência teórica e de uma caracterização plausível de cânones indutivos. Em casos mais restritos, onde uma caracterização da classe de teorias possíveis está disponível e há critérios claros e aplicáveis à igualdade de teorias, argumentos familiares para a subdeterminação falham quando os cânones indutivos são aplicados. Por exemplo, os argumentos bem conhecidos de H. Reichenbach para a subdeterminação da geometria espaço-temporal fracassam quando os cânones indutivos que eu prefiro são aplicados às teorias espaço-temporais.
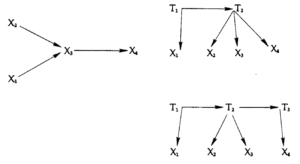
Certamente é verdade que o princípio de explicação que descrevi, mesmo com elaborações sobre necessidade e identidade, é insuficiente como fundamento da lógica indutiva e, se esse princípio fosse o todo, a indeterminação seria de fato galopante. No entanto, o princípio I, em conjunto com outros princípios indutivos disponíveis, pode ser extremamente poderoso e, em alguns contextos, praticamente eliminar a subdeterminação – ou, pelo menos, I conjectura. Considere o contexto fornecido pelo tipo de teoria de Spearman, onde os dados consistem em correlações entre algum conjunto determinado de variáveis. As teorias consistem em quaisquer conjuntos de diagramas sem ciclos, conectando as variáveis mensuráveis entre si ou com variáveis não-mensuráveis e as equações lineares associadas. Sob as suposições sobre erros cometidos antes da equação, elas podem ser reduzidas a equações que relacionam os “coeficientes do caminho” entre si e às correlações mensuradas. As correlações podem satisfazer equações como as equações tétrades de Spearman ou equações análogas que envolvam triplos coeficientes de correlação, quádruplos coeficientes de correlação e assim por diante. Dado um conjunto de dados que satisfaçam determinado conjunto de equações desse tipo, da infinidade de algarismos consistentes com esses dados, um subconjunto adequado reduzirá a verdades matemáticas todas e apenas as equações do conjunto satisfeitas pelos dados. Esse conjunto de diagramas será o preferido pelo princípio 1. Em alguns casos, o conjunto de diagramas preferidos será, acredito, finito e pequeno. Por exemplo, além do diagrama ilustrado em conexão com a explicação de Spearman de suas equações de correlação, conheço apenas três tipos de gráficos direcionados que satisfazem o princípio das três equações de tétrada que Spearman supõe empiricamente. Eles são:
O primeiro diagrama, que não contém variáveis imensuráveis, representa de fato um conjunto inteiro de diagramas, uma vez que quaisquer duas variáveis podem ser intercambiadas sem que se afete a derivação das equações da tétrade. Qualquer um dos diagramas desse tipo pode ser distinto daqueles em que se introduzem variáveis latentes, visto que os diagramas desse tipo impõem restrições em correlações parciais que não estão implícitas pelos diagramas com variáveis latentes. Várias outras restrições empíricas podem distinguir as três alternativas com variáveis não mensuradas em um ou outro no contexto de uma teoria maior. Mesmo quando restrições empíricas não estão disponíveis, não significa que restrições metodológicas não estejam. Em Theory and Evidence, descrevi uma estratégia para testar sistemas de equações algébricas em variáveis reais com coeficientes conhecidos. No contexto de teorias lineares do tipo aqui considerado, os princípios baseados no teste de bootstrap podem não nos levar a preferir teorias com variáveis latentes ou não mensuradas, mas podem levar a preferências determinantes entre um conjunto de teorias que possuem variáveis latentes. Pela suposta equação tétrade de Spearman, temos quatro classes de diagramas teóricos que satisfazem o princípio 1. As correlações parciais podem estabelecer ou eliminar a classe de diagramas que contenha apenas variáveis mensuráveis. Dos três diagramas restantes, o modelo original de Spearman é o preferido dos princípios de bootstrap na ausência de outras informações. Isso ocorre porque os outros dois diagramas contêm implicitamente coeficientes teóricos que não podem ser avaliados a partir de correlações mensuráveis, mesmo assumindo a correção das relações causais que eles postulam. No jargão dos economistas, eles não são “identificáveis”.
Este é apenas um exemplo, e um exemplo conjectural. Pretendo ilustrar nada além de que podem haver muitas surpresas reservadas quando questões de subdeterminação são examinadas de maneiras mais modestas e detalhadas. Atualmente, é certo que não há nenhuma razão específica para acreditar que a subdeterminação seja galopante uma vez que avancemos além do observável. A subdeterminação é, espero, indestrutível de outra maneira, pois a lógica não determina um conjunto único de cânones indutivos, talvez nenhum conjunto de cânones indutivos. Assim, os anti-realistas ainda podem recorrer à negação de princípios ou preferências inferenciais como as que descrevi. Meu ponto não foi apenas dar essa descrição, mas argumentar que os princípios descritos são os que usamos em nossa ciência para concluir sobre o observável e o inobservável. Se tais princípios forem abandonados a tout court, o resultado não será apenas um simples anti-realismo científico sobre o inobservável, mas, em vez disso, um intrincado ceticismo.
Revisão por H&L Revisão e Tradução
Caso o leitor tenha aprendido algo com nossos textos, favor considerar uma doação, via PIX [real] ou Lightning Network [Bitcoin], no código QR correspondente. Sua contribuição nos motiva a continuar fornecendo filosofia de forma simples, mas não simplificada.
Bibliografia:
- Brody – Identity and Essence (Princeton: Princeton Universíty Press, 1980).
- Hempel – “The Theoretician’s Dilemma”, in Aspects of Scientific &planation (Glencoe: Free Press, 1965).
- Hempel and P. Oppenheim – “Studies ín the Logíc of Explanatíon,” em Aspects of Scíentifíc Explanation.
- Spearman – “General Intelligence Objectively Determined and Measured”, American JournaI of Psychology 15 (1904): 201-293.
- P. Duhem – The Aim and Structure of PhysícaI Theory (New York: Atheneum, 1974), e W. V. O. Quine, “Two Dogmas of Empiricism”, em From A Logical Poínt of View (Cambridge: Harvard University Press, 1953).
- R. Eberle, D. Kaplan, e R. Montague – “Hempel and Oppenheím on Explanatíon,” Philosophy of Scíence 28 (1961): 418-428.
- W. Salmon – Statistical Explanation and Statistical Relevance (Píttsburgh: University of Píttsburgh Press, 1971).
- Kaplan – “Explanatíon Revisited, ” Philosophy of Scíence 28 (1961): 429- 436.
- Dumas – Lecons de Philosophíe Chemique (Paris: Gauthier Villars, 1937)
- Friedman – “Explanatíon and Scíentífíc Understandíng”, Journal of Philosophy 72 (1974): 5-19.
- Causey – Unity of Scíence (Dordrecht: D. Reidel, 1979).
O original pode ser acessado em http://fitelson.org/290/glymour.pdf
[1] J. Dumas, Lecons de Philosophíe Chemique (Paris: Gauthier Villars, 1937), 178-179. Essa edição é uma reimpressão (com uma pequena alteração no título) da edição de 1837. [N. do A.]
[2] Para um resumo da querela entre realistas e antirrealistas, acessar este link. [N. do T.]
[3] C. Hempel, “The Theoretician’s Dilemma”, in Aspects of Scientific &planation (Glencoe: Free Press, 1965). [N. do A.]
[4] Cf. P. Duhem, The Aim and Structure of PhysícaI Theory (New York: Atheneum, 1974), e W. V. O. Quine, “Two Dogmas of Empiricism”, em From A Logical Poínt of View (Cambridge: Harvard University Press, 1953). [N. do A.]
[5] C. Spearman, “General lntelligence Objectively Determined and Measured”, American JournaI of Psychology 15 (1904): 201-293. [N. do A.]
[6] No primeiro tipo estão as teorias de Hempel e Oppenhein, D. Kaplan, e mais recentemente, J. Thorpe, B. Cupples e mais alguns outros. No segundo tipo estão teorias com as de Salmon, Brody, Friedman e Causey. E no terceiro há teorias como as de Van Fraassen, B. Skyrms (Acredito eu), P. Achinstein e, recentemente, Putman. [N. do A.]
[7] C. Hempel and P. Oppenheim, “Studies ín the Logíc of Explanatíon,” em Aspects of Scíentifíc Explanation. [N. do A.]
[8] Cf. R. Eberle, D. Kaplan, e R. Montague, “Hempel and Oppenheím on Explanatíon,” Philosophy of Scíence 28 (1961): 418-428. [N. do A.]
[9] D. Kaplan, “Explanatíon Revisited, ” Philosophy of Scíence 28 (1961): 429- 436. [N. do A.]
[10] Cf. W. Salmon, Statistical Explanation and Statistical Relevance (Píttsburgh: University of Píttsburgh Press, 1971). [N. do A.]
[11] M. Friedman, “Explanatíon and Scíentífíc Understandíng”, Journal of Philosophy 72 (1974): 5-19. [N. do A.]
[12] R. Causey, Unity of Scíence (Dordrecht: D. Reidel, 1979). [N. do A.]
[13] B. Brody, Identity and Essence (Princeton : Princeton Universíty Press, 1980). [N. do A.]
[14] Estou em débito com meu aluno Jeanne Kim por me sugerir este exemplo. [N. do A.]
